[ 다익스트라 알고리즘이란? ]
- 다이나믹 알고리즘을 이용하여 최단 거리를 탐색하는 알고리즘
- ROOT 도시에서 다른 도시로 가는 최단 경로를 탐색
강의 안듣고 하다가 개념을 헷갈려서 한참 헤맸네요. 크루스칼 알고리즘이랑 같은 결과는 내는 건줄 알았는데 다른 알고리즘이었습니다. 크루스칼 알고리즘이 전체 경로를 최단 거리로 만들어주는 것이라면, 다익스트라 알고리즘은 ROOT 도시에서 각 도시로 가는 최단 경로를 탐색하는 알고리즘입니다. 즉, 크루스칼보다 다익스트라의 결과값이 더 크게 나올 수 있게 됩니다.
예를 들어 아래 그림에서 0번 도시에서 5번 도시로 가는 경우 다익스트라 알고리즘에서는 가장 짧은 거리인 0-1-5 입니다. 하지만 크루스칼에서는 전체 경로의 효율성을 고려하여 0-1-6-5의 경로를 채택하게 됩니다.
크루스칼 알고리즘 때와 같은 데이터를 사용했습니다. 크루스칼 때와는 달리 거리 순으로 정렬할 필요가 없기 때문에 2차원 배열을 사용했습니다. 물론 구조체로 무방하긴 합니다만 더 헷갈려지더라구요.
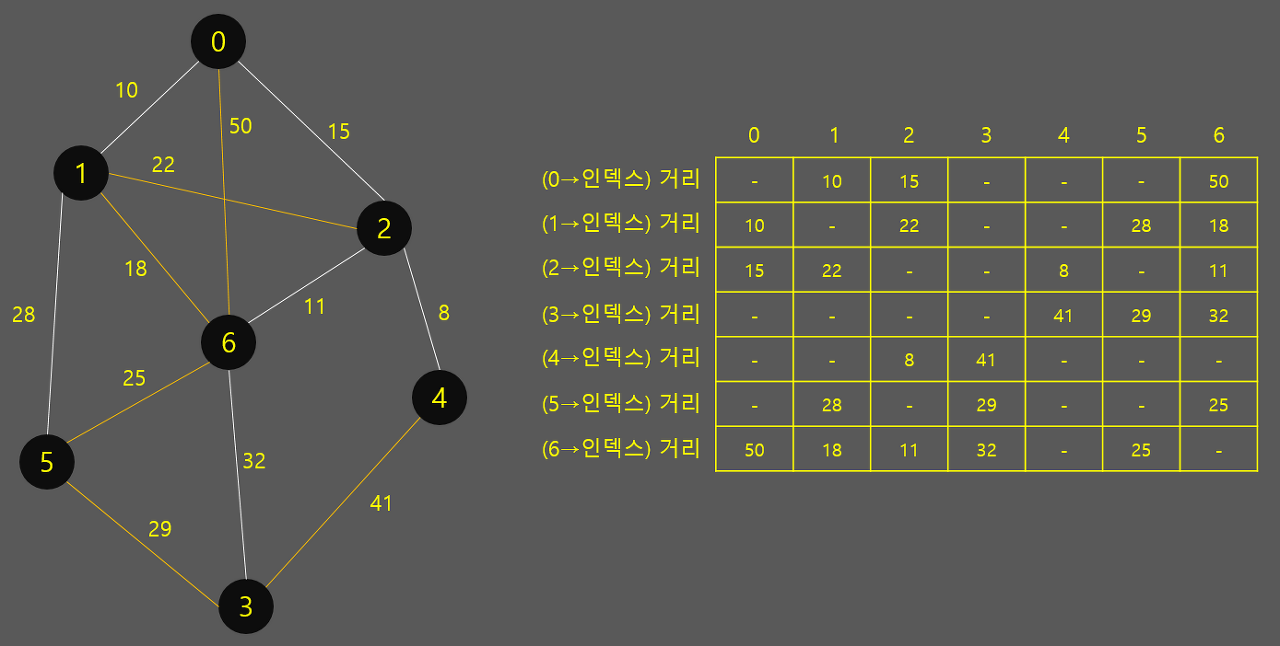
알고리즘의 핵심은, 루트 도시(현재 0번 도시)에서 다른 도시로 가는 길 중 최단 거리를 갱신해나가면서 찾아나가는 것입니다. 아래와 같이 현재 0번 도시에서 각 도시로 갈 수 있는 최단 거리를 표시해둔 뒤 계속 갱신해 나가는 것이죠. dist[0~6] 배열은 따로 안만들고 2차원 배열의 h[0][0~6]을 바로 수정해도 됩니다. 헷갈릴까봐 하나 더 만들었는데 굳이 그럴 필요는 없을 것 같네요.

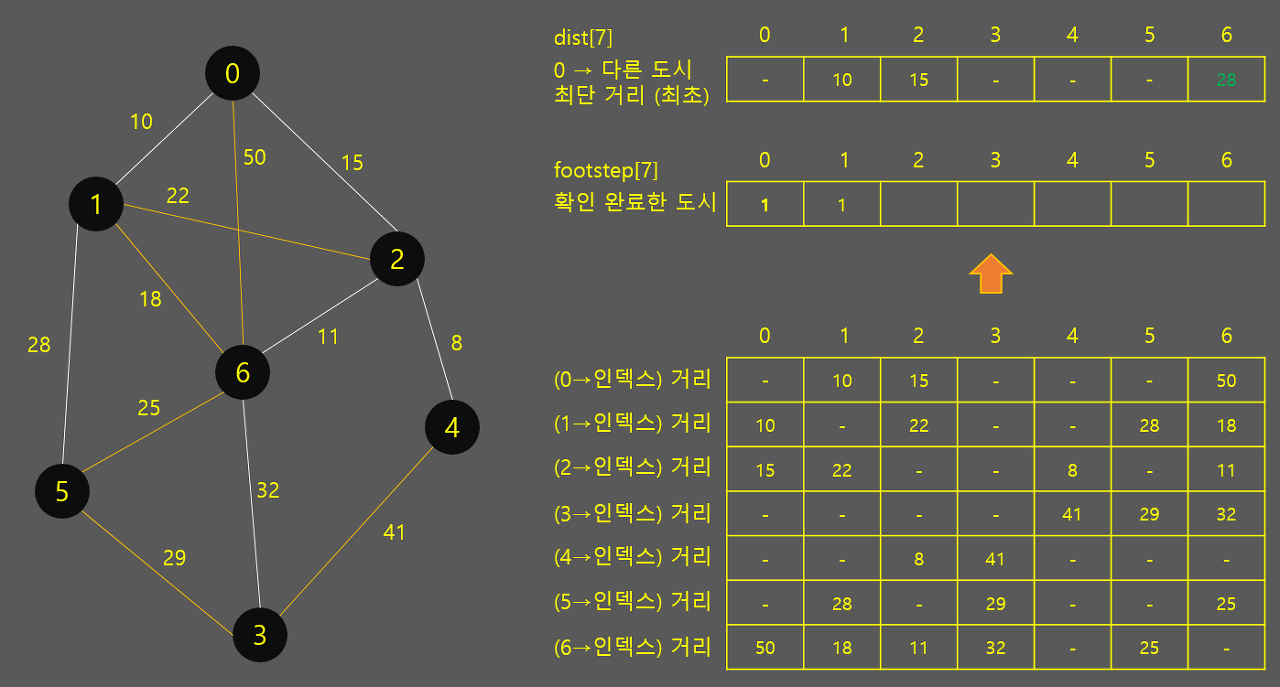
dist[7]의 거리 중, 가장 짧은 거리를 찾아 시작합니다. 순서야 그리 중요한 건 아니지만 이미 연결돼 있는 도시를 기준으로 찾아나가야 하고, 어차피 최단 거리를 찾는 로직이니 최단 거리 순으로 움직이는 것이 가장 효율적입니다.
최단 거리인 1번 도시로 가서 확인을 하면 아래와 같이 최단거리가 갱신됩니다. 현재 1로 가는 최단 거리가 dist[1]의 값인 10이기 때문에 '10 + h[1][6] == 28'이 dist[6]의 값이 50보다 작기 때문에 갱신이 되는 구조입니다. 나중에 어느 다른 도시를 방문하더라도, 일단 현재 0→x번 도시로 가는 최단 경로는 dist[]의 값이라는 것만 유의하면 어렵지 않게 코드로 풀어낼 수 있습니다.

코드는 아래와 같습니다. 강의 코드는 강의 듣고 아래에 추가하겠습니다.

#include <stdio.h>
#define SIZE 7
typedef struct {
int upcity;
int dist;
}c;
void dijkstra_find(c* city, int h[][SIZE], int* dist);
int min_find(int* footstep, int* dist);
void main()
{
/* 도로 정보 */
int h[][SIZE] = {
{0,10,15,0,0,0,50},{0,0,22,0,0,28,18},{0,22,0,0,8,0,11},
{0,0,0,0,41,29,32},{0,0,8,41,0,0,0},{0,28,0,29,0,0,25},{0,18,11,32,0,25,0}};
/* 도시 정보 */
c city[SIZE];
/* 0->다른 도시 간 거리 정보 */
int dist[SIZE] = { 0 };
/* 최단거리 찾기 */
dijkstra_find(city, h, dist);
printf("\n");
/* 출력 */
for (int i = 0; i < SIZE; i++)
printf(" %d번도시 - 상위도시 : %d 최종 거리 : %d\n",
i, city[i].upcity, city[i].dist);
printf("\n ");
}
/* 다익스트라 알고리즘 길찾기 */
/* parameter : 도시정보 city, 거리정보 h, 최단거리 저장 dist */
/* return : void */
void dijkstra_find(c* city, int h[][SIZE], int* dist)
{
int footstep[SIZE] = { 1, 0 }; // 방문완료한 도시 (0번 도시는 방문처리)
for (int i = 0; i < SIZE; i++) // 첫 배열 복사 (0에서 연결된 도시 정보)
{
dist[i] = h[0][i];
city[i].upcity = 0;
city[i].dist = dist[i];
}
/* 도시를 다 방문할 때까지 반복문 수행 */
int i;
while ((i = min_find(footstep, dist)) != -1)
{
footstep[i] = 1; // 방문처리
for (int j = 1; j < SIZE; j++)
{
/* 새로운 길이 현재 저장된 값보다 더 작거나 0인 경우 갱신 */
if (h[i][j] != 0 && (dist[i] + h[i][j] < dist[j] || dist[j] == 0))
{
dist[j] = dist[i] + h[i][j];
city[j].upcity = i;
city[j].dist = dist[j];
}
}
}
}
/* 방문하지 않은 도시 중 가장 적은 값의 노드를 찾음 */
/* parameter : 방문도시 footstep, 현재 거리정보 dist */
/* return : 가볼 도시가 있을 경우 최소값 노드의 도시, 없을 경우 -1 */
int min_find(int* footstep, int* dist)
{
int min = 999999;
int j = -1;
for (int i = 1; i < SIZE; i++)
if (dist[i] != 0 && dist[i] < min && footstep[i] == 0)
{
min = dist[i];
j = i;
}
if (j == -1) // 모두 방문했을 경우
return -1;
else // 방문할 도시가 남은 경우
return j;
}
강의 코드에서는 최소값을 찾는 부분을 C++ 라이브러리를 이용해서 정렬 후 진행하네요. 간선과 도시가 많아 질수록 최소값을 찾기 위한 시간 복잡도가 배가 되니 줄이는게 맞다고 합니다. C++ 코드로 진행돼서 강의코드는 스킵하겠습니다. 만약 제가 고치게 된다면 그냥 크루스칼 알고리즘때처럼 구조체를 사용하는 방식으로 자료구조를 손보는게 좀 더 효율적일 것 같다는 생각이 듭니다. 만약 도시가 만개라면, h[10000][10000]의 배열을 만드는건 너무 비효율적이니까요. 비어있는 값이 없도록 구조체 연결리스트를 사용하면 좋을 것 같습니다~!
'▸C언어 > 알고리즘 및 자료구조' 카테고리의 다른 글
| 위상 정렬 [1/1] (0) | 2019.12.09 |
|---|---|
| 플로이드 와샬 알고리즘_최단경로 길찾기 [1/1] (0) | 2019.12.09 |
| 에라토스테네스의 체_소수 찾기 [1/1] (1) | 2019.12.09 |
| 다이나믹 알고리즘_타일 채우기 [2/2] (0) | 2019.12.09 |
| 다이나믹 알고리즘_타일 채우기 [1/2] (0) | 2019.12.09 |


댓글