[ 플로이드 와샬 알고리즘이란? ]
- 다익스트라 알고리즘의 반복 수행과 동일한 결과
- 모든 도시를 ROOT로 뒀을 때의 결과를 다익스트라보다 더 효율적으로 구할 수 있음
기본적으로 다익스트라 알고리즘에서 모든 ROOT 도시에 대한 최단 거리를 구하기 위해 조금 수정됐다고 볼 수 있습니다. 다익스트라는 출발도시를 기준으로 하고, 플로이드 와샬은 거쳐가는 도시를 기준으로 한다고 되어 있지만, 사실 다익스트라도 거쳐가는 도시를 기준으로 하고 있습니다. 다만 거쳐가는 도시를 탐색할 순서를 "루트도시를 기준으로 아직 방문하지 않은 최단 거리 도시"로 선정해서 수행하는 거죠.

즉 다익스트라에서도 1번을 거쳤을 때 다른 도시로 갈 수 있는 거리, 2번을 거쳤을 때, 6번을 거쳤을 때... 로 순서를 지정해 줘서 다른 도시로 가는 최단 경로를 찾는 방식입니다.
하지만 모든 도시를 ROOT 도시로 할 때를 가정하면 굳이 순서를 지정해줄 필요가 없습니다. 모든 출발도시에서 1번 도시를 거칠 때의 비용, 모든 출발도시에서 2번 도시를 거칠때의 비용... 으로 모든 도시를 거칠 때의 비용을 계속해서 갱신해주면 되는 것이죠.
순서를 지정하는 연산이 필요가 없다는 점에서 다익스트라를 반복하는 것보다 더 효율적으로 모든 도시를 ROOT도시로 뒀을 때의 최단거리를 구할 수 있게 되는 것입니다. 직접 코딩하면서 해보시면 알겠지만 플로이드 와샬 알고리즘을 통해 어느 한 ROOT도시의 최단거리만 구해보려고 하면 결국 다익스트라 알고리즘처럼 짤 수 밖에 없게 됩니다.
직관적으로 이해는 좀 어려웠지만 구현 방식 자체는 매우 쉽습니다.

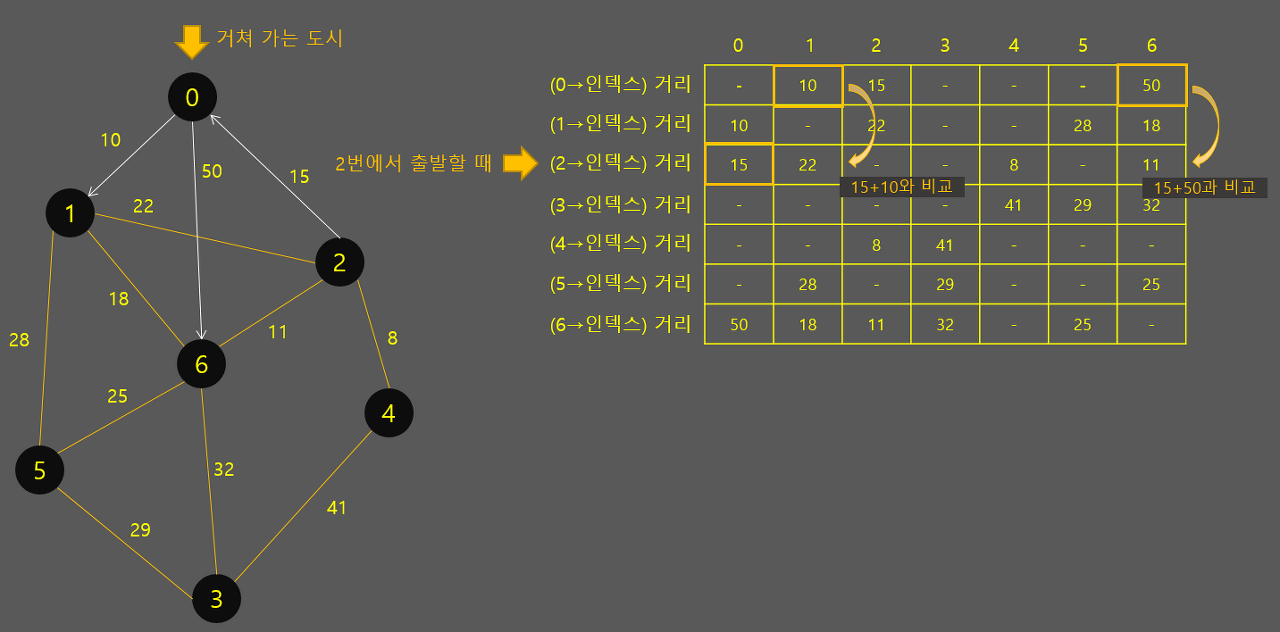
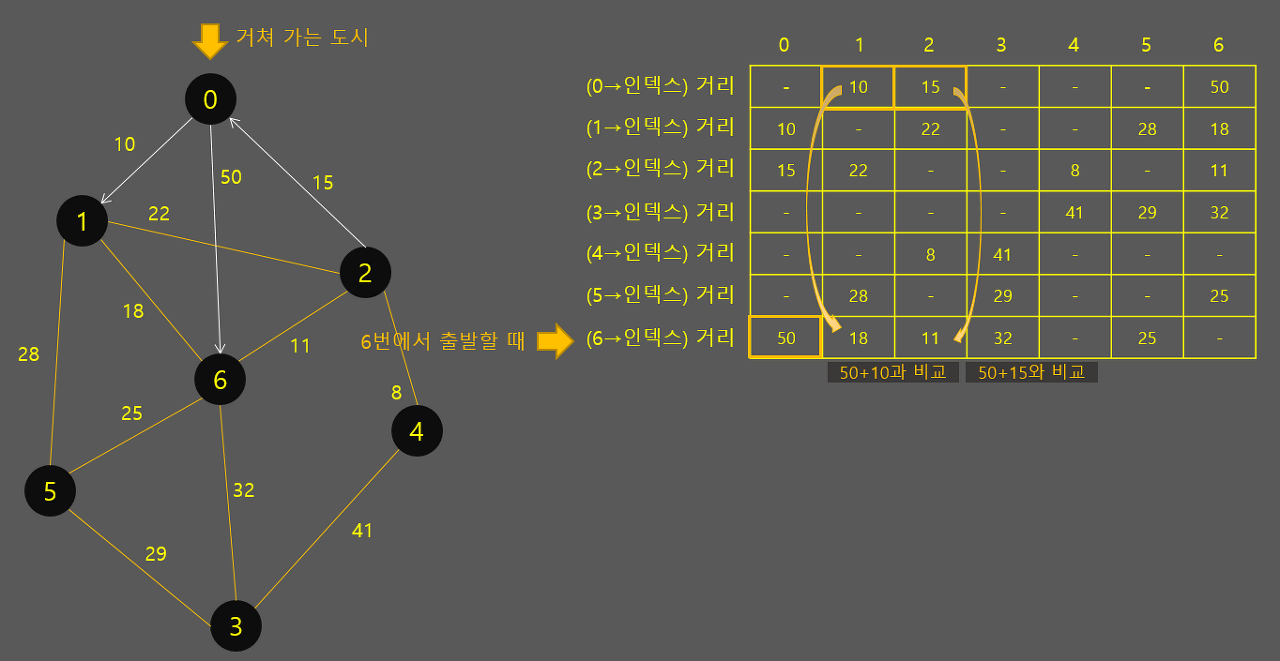
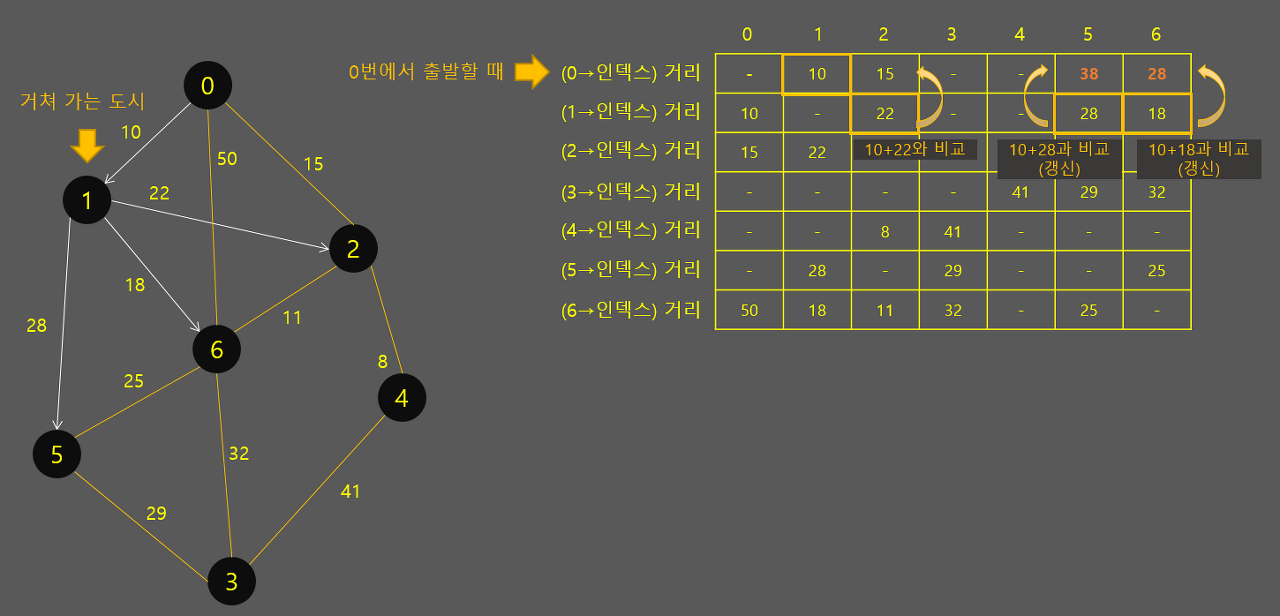
이런식으로 하나의 도시를 거쳐간다고 했을 때, 다른 모든 도시들이 출발지가 돼서, 그 도시를 거쳐갔을 때 다른 도시로 가는 비용을 비교해보는 것입니다. 계속 갱신해 나가면 됩니다. 다익스트라보다 오히려 코드가 간결해지는 것을 알 수 있습니다.
다만 3중 for문이 빈틈없이 돌기 때문에 시간복잡도가 O(n^3)입니다. 제 생각엔 다익스트라 알고리즘의 자료구조를 정렬된 연결리스트 형식으로 바꿔서 시간복잡도를 낮추면 플로이드 와샬보다 훨씬 빠른 로직으로 만들 수 있을 것 같습니다. 자료구조와 알고리즘의 적절한 조화가 중요한 이유가 되겠네요.

#include <stdio.h>
#define SIZE 7
#define M 999999
void floyd_warshall(int h[][SIZE]);
void main()
{
/* 도로 정보 */
int h[][SIZE] = {
{0,10,15,M,M,M,50},{10,0,22,M,M,28,18},{15,22,0,M,8,M,11},
{M,M,M,0,41,29,32},{M,M,8,41,0,M,M},{M,28,M,29,M,0,25},{50,18,11,32,M,25,0} };
/* 최단거리 찾기 */
floyd_warshall(h);
/* 출력 */
for (int i = 0; i < SIZE; i++)
{
printf("\n ");
for (int j = 0; j < SIZE; j++)
printf("%d ", h[i][j]);
printf("\n");
}
}
/* 플로이드 와샬 알고리즘 길찾기 */
/* parameter : 거리정보 h*/
/* return : void */
void floyd_warshall(int h[][SIZE])
{
for (int c = 0; c < SIZE; c++) // 거쳐갈 도시
for (int b = 0; b < SIZE; b++) // 출발 도시
{
// 거쳐갈 도시와 출발 도시가 같다면 넘어감
if (c == b) continue;
for (int a = 0; a < SIZE; a++) // 도착 도시
{
// 거쳐가는 경우가 더 빠른 경우 갱신
if (b != a && h[c][a] != 0 && h[b][c] + h[c][a] < h[b][a])
h[b][a] = h[b][c] + h[c][a];
}
}
}'▸C언어 > 알고리즘 및 자료구조' 카테고리의 다른 글
| 문자열 찾기(매칭)_KMP알고리즘 [1/2] (0) | 2019.12.09 |
|---|---|
| 위상 정렬 [1/1] (0) | 2019.12.09 |
| 다익스트라 알고리즘_최단경로 길찾기 [1/1] (0) | 2019.12.09 |
| 에라토스테네스의 체_소수 찾기 [1/1] (1) | 2019.12.09 |
| 다이나믹 알고리즘_타일 채우기 [2/2] (0) | 2019.12.09 |


댓글