[ 이분탐색이란? ]
- 정렬된 데이터에서 특정 값을 찾을 때, 하나하나 찾는것이 아니라 범위를 좁혀나가며 찾는 방법
- O(logN)의 시간 복잡도가 소요되어 정렬되어 있는 데이터를 보다 빠르게 검색 가능
이미 정렬이 되어 있다는 것은 처음부터 찾아나가는 것 보다 더 효율적인 탐색 방법이 항상 존재합니다. 그 중 가장 간단한 방법인 이분 탐색을 해도 해도 항상 헷갈리는 재귀함수 사용법과 함께 정리해봅니다.
먼저 정렬된 데이터가 있습니다. size를 구하고 찾을 데이터를 입력합니다. 배열에서 범위를 지정할 때는 대부분 size를 사용하는 것이 편합니다. 예를 들어 10개가 있으면 배열의 마지막 인덱스는 9이지만 총 10개라 size는 10이 됩니다.

int arr[] = { 1,2,5,7,11,15,22,38,99,101 };
int size = sizeof(arr) / sizeof(int);
int find = 38;
이제 이분탐색 함수를 하나 만듭니다. 배열과 size정보, 시작지점(start)과 끝지점(end)을 받습니다. 참고로 배열 정보를 함수에서 parameter로 받을 경우, 그 배열의 시작점 주소만을 받기 때문에 함수 안에서 size를 구할 수는 없습니다. 함수 안에서 sizeof(arr)을 해보면 포인터변수 크기인 4Byte만 알 수 있습니다.
int binary_search(int find, int* arr, int start, int end);
int main()
{
int arr[] = { 1,2,5,7,11,15,22,38,99,101 };
int size = sizeof(arr) / sizeof(int);
int find = 38;
}
이제 아래와 같이 범위를 반씩 계속 쪼개나가면서 값을 찾아나갑니다. 일정한 규칙으로 함수에 arguments를 전달하는 것은 일반 반복문으로 쉽게 됩니다. 하지만 지금 같은 경우, 찾을 데이터에 따라 범위가 왼쪽이 될 수도, 오른쪽이 될 수도 있기 때문에 이렇게 어떤 조건에 따라 함수에 제공해 줄 arguments가 계속 바뀔 때는 재귀함수를 써주는 것이 여러모로 편리합니다.
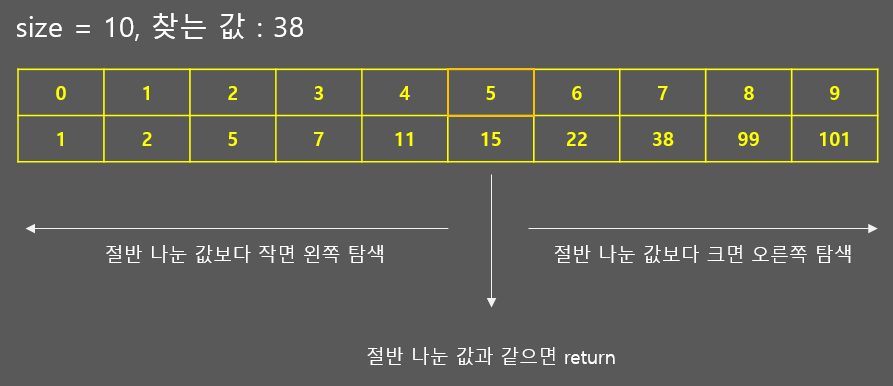
이제 해당 로직을 반복수행할 재귀함수를 작성합니다. 재귀함수 사용 시에는 항상 탈출조건을 먼저 생각하는 것이 좋습니다.
※ 탈출조건
1. 절반으로 나눈 값(범위의 가장 중간에 있는 값)이 찾는 값과 일치할 때
2. 1번을 만족하지 않는데 start가 end보다 작거나 같아질 때
1번은 당연한거니까 2번을 살펴보겠습니다. 예시에서 만약 배열에 없는 '39'를 찾는다고 가정하겠습니다. 중간 값보다 찾는 값이 크다면 오른쪽 범위를 던져줍니다. 즉, "(중간값 + 1) ~ end" 범위가 됩니다. 중간 값보다 작다면 왼쪽 범위를 던져줍니다. "start ~ (중간값 - 1)" 범위가 됩니다.

"중간값 = (start + end) / 2"로 구할 수 있으므로, 오른쪽으로 계속 찾다 보면 범위가 하나의 숫자로 압축되어 "start == end" 가 되는 지점이 발생합니다. 또한 왼쪽으로 찾다가 범위가 2개로 좁혀지는 경우에는 중간값이 두 개 중 앞의 숫자가 되므로 "start > end"가 되는 지점이 발생합니다. 이 경우를 마지막에 도달했을 때의 탈출조건으로 지정해주면 됩니다. 물론 그냥 "start == end"조건 없이 "start > end"만 써도 동일하게 작동합니다. (한 번 그려보면 쉽게 이해가 갑니다. 다만 딱 1번만큼 재귀함수를 더 사용하게 됩니다. ㅎㅎ)
즉, 1번 탈출조건을 먼저 확인하고 아닐 경우 2번 탈출조건을 확인하면 됩니다. 범위를 이용하는 재귀함수에서는 대부분 비슷한 로직이 적용됩니다. 값을 찾았을 때, 또는 마지막에 도달헀을 때 두 가지를 재귀함수의 탈출 조건으로 주면 됩니다.


탈출 조건이 명확해졌으면 그대로 코드로 옮깁니다.
#include <stdio.h>
int binary_search(int find, int* arr, int start, int end);
int main()
{
int arr[] = { 1,2,5,7,11,15,22,38,99,101 };
int size = sizeof(arr) / sizeof(int);
int find = 0;
}
int binary_search(int find, int* arr, int start, int end)
{
int s = (start + end) / 2; // 중간 값 (middle)
if (arr[s] == find) // 같으면 해당 인덱스 리턴
return s;
else if (start >= end) // 마지막 하나로 압축됐는데 위 1번 탈출 조건을
return -1; // 충족시키지 못해 여기로 왔으면 못찾음(-1) 리턴
}
이제 탈출은 컴퓨터가 알아서 할 것이므로 중간값보다 크면 오른쪽으로 범위를 지정해주고, 작으면 왼쪽으로 범위를 지정해서 동일 로직을 반복하는 재귀함수를 짜면 됩니다.
여기서 한 가지 팁은 void함수가 아닌 return값이 있는 함수를 재귀함수로 사용했을 때, 마지막에 도달한 함수의 return값을 최종적으로 받아오기 위해서는 재귀함수 자체를 return 값으로 사용해야한다는 것입니다.
재귀함수는 하나의 함수로 들어갈 때마다 전혀 다른 스택 메모리에 쌓이기 때문에 함수가 종료되면 모든 변수가 사라집니다. 즉, 재귀함수가 바깥 재귀함수에게 값을 전달해주는 방법은 포인터변수 또는 전역변수를 이용해서 바깥에 있는 변수를 조작주는 방법이 아니면 return값으로 값을 되돌려주는 방법 두 개 밖에 없습니다.
함수를 열 번 타고 들어갔다고 하면 마지막에 함수가 리턴한 값을 첫번 째 함수가 알 수 있도록 하려면 계속 함수 자체가 return값이 되어야 한다는 의미입니다. 그럼 마지막 범위를 줄이는 코드를 짜보면 코드가 완성됩니다.

#include <stdio.h>
int binary_search(int find, int* arr, int start, int end);
int main()
{
int arr[] = { 1,2,5,7,11,15,22,38,99,101 };
int size = sizeof(arr) / sizeof(int);
int find = 38;
int result = binary_search(find, arr, 0, size);
if (result == -1)
puts("\n 찾을 수 없습니다.");
else
printf("\n %d번째에 있습니다\n", result + 1);
}
int binary_search(int find, int* arr, int start, int end)
{
int s = (start + end) / 2; // 중간 값 (middle)
if (arr[s] == find) // 같으면 해당 인덱스 리턴
return s;
else if (start >= end) // 마지막 하나로 압축됐는데 위 1번 탈출 조건을
return -1; // 충족시키지 못해 여기로 왔으면 못찾음(-1) 리턴
else if (find < arr[s])
return binary_search(find, arr, 0, s - 1);
else if (find > arr[s])
return binary_search(find, arr, s + 1, end);
return -1;
}
'▸C언어 > 알고리즘 및 자료구조' 카테고리의 다른 글
| 이분매칭_작업 할당하기[1/1] (0) | 2019.12.09 |
|---|---|
| 문자열 찾기(매칭)_라빈 카프 알고리즘 [2/2] (0) | 2019.12.09 |
| 문자열 찾기(매칭)_KMP알고리즘 [1/2] (0) | 2019.12.09 |
| 위상 정렬 [1/1] (0) | 2019.12.09 |
| 플로이드 와샬 알고리즘_최단경로 길찾기 [1/1] (0) | 2019.12.09 |


댓글